How Much CO2 Is Produced During Fermentation?
Share
So, the other day I was wondering if the CO2 coming out of my fermenter could be used in two ways.
Currently I use a spunding valve (adjustable pressure relief valve) on the gas post of my Fermzilla (a pressurisable plastic fermetation vessel with standard keg fittings on top for gas and liquid connections).
By setting this at what I would usually set my regulator at to force carbonate the beer after it finishes fermenting I keep the beer at that pressure during fermentation using the CO2 produced. This means that when primary fermentation is complete the beer is already carbonated and just needs to be chilled!
However there is still a bunch of CO2 that blows out of the spunding valve while the fermentation is active and I thought... "I wonder if there is enough there to flush out all my kegs etc too?"
Well, I found the maths online and turn out that YES, there absolutely is!
I've copied and pasted the maths from an article below that I found by Dennis from the blog Life, Fermented but basically the outcome is....
A standard 20L brew produces between 400 and 600L of CO2!!!
So now on the blow off side of my spunding valve I attach a line with a gas disconnect on it and use that to push sanitiser through my kegs, lines, taps etc and leave them full of CO2 during the first few days of fermentation. This means they are ready for kegging the brew when the brew is ready with no cost of extra gas to me plus a little bit of help to reduce the carbon footprint of my brewing.
The Maths - Taken From Life Fermented
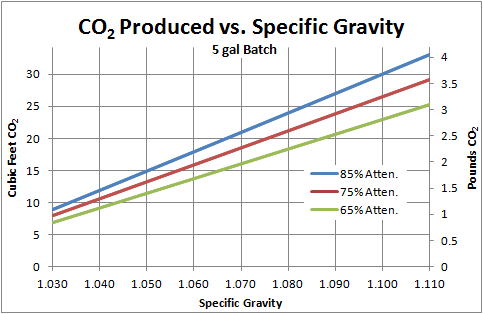
"The results of my calculations are presented here, in both English and metric units. Below I give a bit more detail on the actual calculations. If you look at the plots, you’ll notice that not only is the volume of gas large (left axis), the weight of the gas (right axis) is also quite appreciable. Yes, your fermentor looses weight over the course of the brew! In fact, some people have proposed monitoring the attenuation of a batch of beer in real time by monitoring the weight of the fermentor. I always assumed you would need an extremely precise scale, but it turns out the difference is so large, you actually wouldn’t.
For anyone interested in the math behind the plots, read on.
The first thing I did was to convert specific gravity (SG in 1.xxx format) to degrees Plato (°P) with the equation . This is a third order polynomial fit derived from the American Society of Brewing Chemists gravity to Plato tables, given on en.wikipedia.org/wiki/brix. This is a convenient unit to work in because every 1°P is 1% by weight sugar, so a 1.060 SG wort would be 14.741°P, or 14.741% sugar by weight.
To find the mass of sugar in each wort, I then found the weight of a 5 gal/ 18.9 L batch by multiplying this volume by its density (if working in metric, this amounts to simply multiplying by the specific gravity since water is 1 kg/L). Then, its a simple matter of multiplying by the sugar weight percent. The example 1.060 wort contains (44.23 lb wort)*(0.14741)= 6.52 lb or 2.96 kg sugar. Note that I actually did all of my calculations in metric, then converted to English because the units work out so nicely.
Next, we must find how much sugar is actually consumed. For this, remember that the “attenuation” used most often is “apparent attenuation” as measured by a hydrometer. Hydrometers actually measure the density of the solution, so when alcohol is created (its density is lower than water), the hydrometer is tricked into thinking more of the sugar has been consumed than really was. Actual attenuation can by found by multiplying the apparent attenuation by 0.814, as given in Greg Noonan’s New Brewing Lager Beer. So the actual amount of sugar consumed in a 1.060 75% apparent attenuation beer is (6.52 lb)(0.75*0.814)= 3.98 lb or 1.81 kg.
Now we must bring in some very basic chemistry. Lets assume this sugar is all (or could become) glucose. A single mole (in units of mol) of glucose weighs 180.156 g or 6.35 oz. A mole is simply a way to keep track of how many molecules of something there is so you can predict chemical reactions. Basically, there are a different number of molecules of acid in vinegar in a gram than the number of baking soda molecules in a gram, but reactions happen to molecules. So to have a complete reaction, you need to add the same number of molecules of acid in vinegar and baking soda, not the same number of grams of each. The upshot is we have (1.81 kg)/(0.180156 kg/mol)=10.02 mol glucose consumed in this example wort.
For every 1 mol glucose consumed, 2 mol of ethanol and 2 mol of CO2 are produced. Thus we have 10.02*2=20.04 mol of total CO2 produced from fermenting this 1.060 wort to 75% apparent attenuation.
Now we can put this in terms of volume or mass of gas. For any “ideal” gas, its volume can be predicted by the ideal gas law at standard temperature and pressure, , where P is pressure (1 atm or atmospheres), V is volume (liters or L), n is the number of moles of gas (1 mol), R is the ideal gas constant (0.0821 (atm*L)/(mol*K)), and T is the temperature (273 Kelvin or K). Solving for volume and plugging in the numbers, we get
. Thus every mol of gas occupies 22.41 L or 0.791 cubic feet. This would be (20.04 mol)*(22.41 L/mol)=449.1 L or 15.86 ft3 of CO2 produced for our example beer. Put another way, from 5 gallons of 1.060 SG wort, you could fill the glass carboy its in almost 24 times with the CO2! In the most extreme case shown on the graph (1.110 wort, 85% attenuation), this more than doubles.
To find the mass of the gas, we simply use the mass of a mole of CO2, 0.04401 kg/mol, to convert back. We have (20.04 mol)*(0.04401 kg/mol)=0.88 kg or 1.94 lb of CO2 produced.
– Dennis,
Life, Fermented